一文详解头部位姿估计【建议收藏】
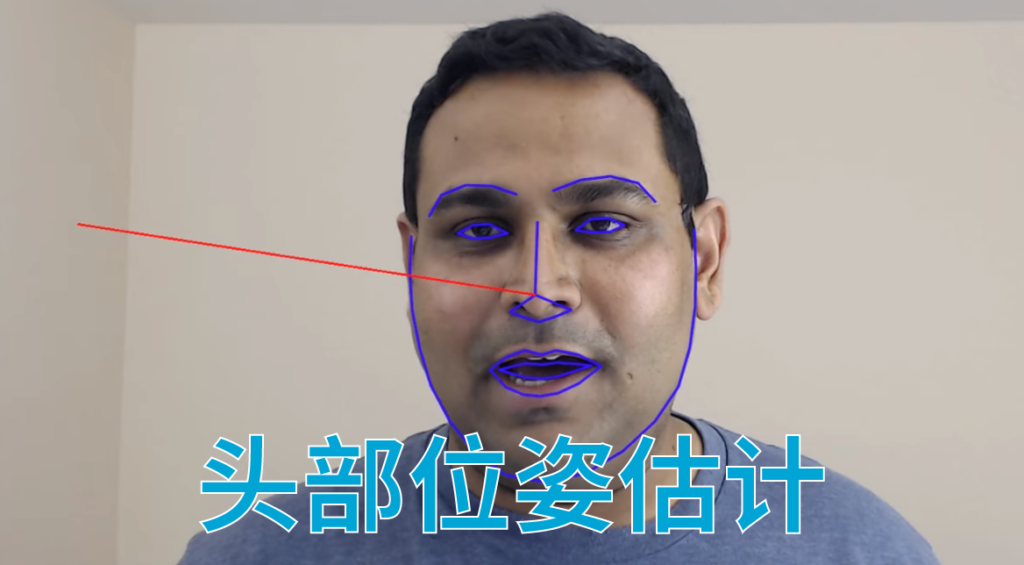
在许多应用中,我们需要知道头部相对于相机是如何倾斜的。例如,在虚拟现实应用程序中,可以使用头部的姿势来渲染场景的正确视图。在驾驶员辅助系统中,汽车上的摄像头可以观察驾驶员的面部,通过头部姿态估计来判断驾驶员是否在关注道路。当然,人们也可以使用基于头部姿势的手势来控制免提应用程序。
本文中我们约定使用下面术语,以免混淆。
位姿: 英文是pose, 包括位置和姿态。
位置: 英文是location 。
图片: 英文是photo ,本文中用来指一幅照片。
图像: 英文是image, 本文中用在平面或坐标系中,例如image plane 指图像平面, image coordinate system 指图像坐标系统。
旋转: 英文是rotation 。
平移: 英文是translation。
变换: 英文是transform 。
投影: 英文是project 。
1、什么是位姿估计?
在计算机视觉中,物体的姿态是指物体相对于相机的相对方向和位置。你可以通过物体相对于相机移动,或者相机相对于物体移动来改变位姿。—— 这二者对于改变位姿是等价的,因为它们之间的关系是相对的。

本文中描述的位姿估计问题通常被称为“Perspective-n-Point” 问题,或计算机视觉中的PnP 问题。PnP 问题的目标是找到一个物体的位姿,我们需要具备两个条件:
条件1: 有一个已经校准了的相机;
条件2: 我们知道物体上的n 个3D 点的位置locations 和这些3D 点在图像中相应的2D 投影。
2、如何在数学上描述相机的运动
一个3D 刚体(rigid object) 仅有2 种类型的相对于相机的运动。
第一种: 平移运动(Translation)。平移运动是指相机从当前的位置location 其坐标为(X, Y, Z)移动到新的坐标位置(X‘, Y’,Z‘)。平移运动有3 个自由度——各沿着X,Y,Z 三个轴的方向。平移运动可以用向量t = (X’-X, Y’-Y, Z’-Z)来描述。
第二种:旋转运动(Rotation)。是指将相机绕着X,Y,Z 轴旋转。旋转运动也有3个自由度。有多种数学上的方法描述旋转运动。使用欧拉角(横摇roll, 纵摇pitch, 偏航yaw)描述, 使用3X3 的旋转矩阵描述,或者使用旋转方向和角度(directon of rotation and angle)。
因此,3D 物体的位姿估计其实就是指寻找描述平移和旋转的6 个数。
3、进行位姿估计时你需要什么?
为了计算一幅图像中一个刚体的3D 位姿, 需要下面的信息:
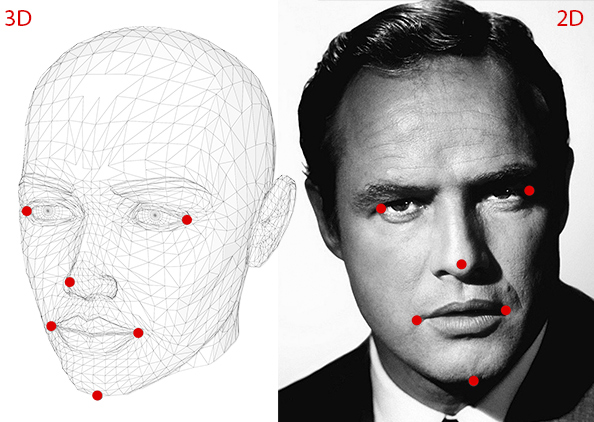
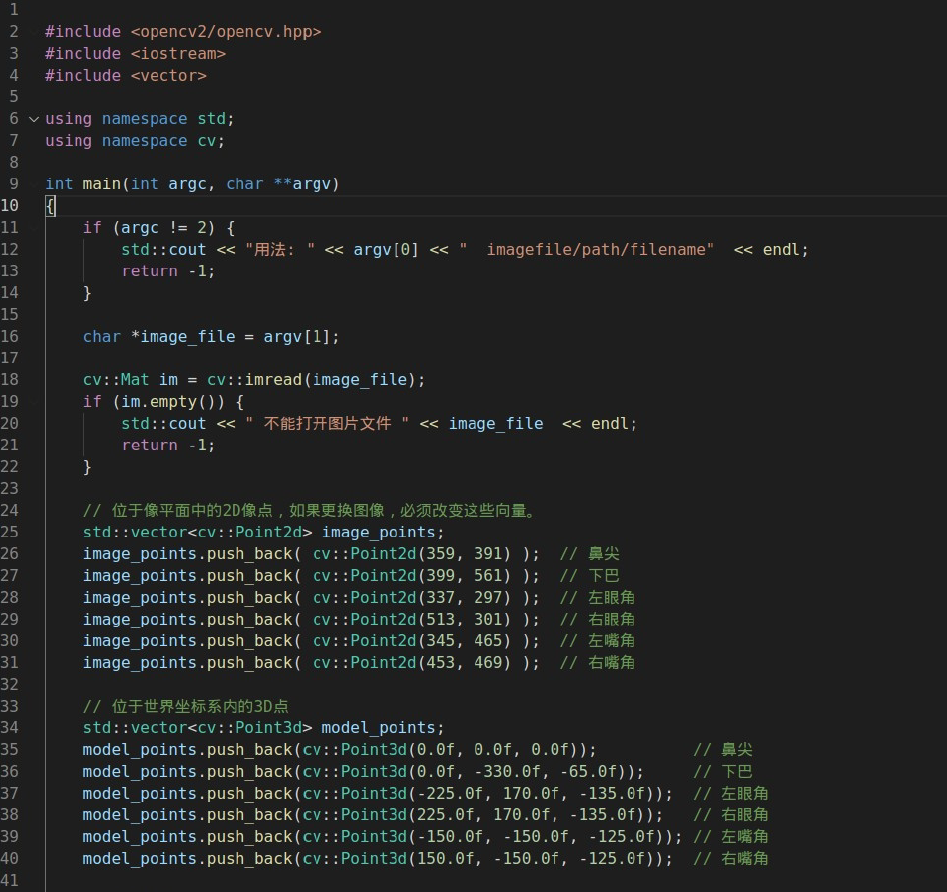
信息1: 若干个点的2D 坐标。你需要一幅图像中若干个点的2D(x, y)位置locations。在人的面部这个例子中,你可以选择:眼角、鼻尖、嘴角等。在本文中,我们选择:鼻尖、下巴、左眼角、右眼角、左嘴角、右嘴角等6 个点。
信息2: 与2D 坐标点一一对应的3D 位置locations。你需要2D 特征点的3D 位置locations。你也许认为,你需要图片中那个人的3D 模型,以便获得3D 位置locations。理想情况下的确如此,但是现实中,情况并非如此。一个3D 模型的确足够了,但是你从哪里搞到一个头部的3D 模型呢?——我们并非需要一个完整的3D 模型!我们仅仅需要在某个任意参考系下若干个点的3D 位置【Just need the 3D locations of a few
points in some arbitrary reference frame】。注意:这里的“某个任意参考系in some arbitrary reference frame”是重点。
在本文中,我们选取的是如下3D 点:
(1)鼻尖(0.0, 0.0, 0.0)。X、Y、Z 坐标都为0.0 意味着这是原点。请思考,这是那个坐标系的原点呢?是相机坐标系?还是世界坐标系?
(2)下巴(0.0, -330.0, -65.0)。
(3)左眼角(-225.0, 170.0, -135.0) 。
(4)右眼角(225.0, 170.0, -135.0) 。
(5)左嘴角(-150.0, -150.0, -125.0) 。
(6)右嘴角(150.0, -150.0, -125.0) 。
注意: 上面的点是在“某个任意参考系/坐标系统in some arbitrary reference frame / coordinate system”中的,该坐标系就算所谓的“世界坐标系World Coordinates”。在OpenCV 文档中,也被称为“模型坐标系Model Coordinates”。
信息3: 相机的内参。正如前文说提到的,在这个PnP 问题中,我们假定相机已经被标定了。换句话来说,你需要知道相机的焦距focal length、图像的光学中心、径向畸变参数。—— 所以,你需要标定你的相机。当然,对我们这些喜欢偷懒的人来说,这个工作太繁琐。有没有能偷懒的办法呢?的确有!
由于没有使用精确的3D 模型,我们已经处于近似状态下。我们还可以进一步进行近似处理:(1)我们可以用图像中心近似光学中心;(2)用图像的像素宽度近似相机的焦距;(3)假定不存在径向畸变。
4、位姿估计算法是如何工作的?
有很多的位姿估计算法,最有名的可以追溯到1841 年。该算法的详细讨论超出了本文的讨论范围。这里只给出其简要的核心思想。
该位姿估计PnP 问题涉及到3 个坐标系统。(1)世界坐标系。前面给出的各个面部特征的3D 坐标就是在世界坐标系之中;(2)如果我们知道了旋转矩阵R 和平移向量t ,我们就能将世界坐标系下的3D 点“变换Transform” 到相机坐标系中的3D 点。(3)使用相机内参矩阵,能将相机坐标系中的3D 点能被投影到图像平面image plane, 也就算图像坐标系统image coordinate system。
整个问题就是在3 个坐标系统中玩耍: 3D 的世界坐标系World coordiantes、3D的相机坐标系Camera coordinates、2D 的图像坐标系Image coordinates。
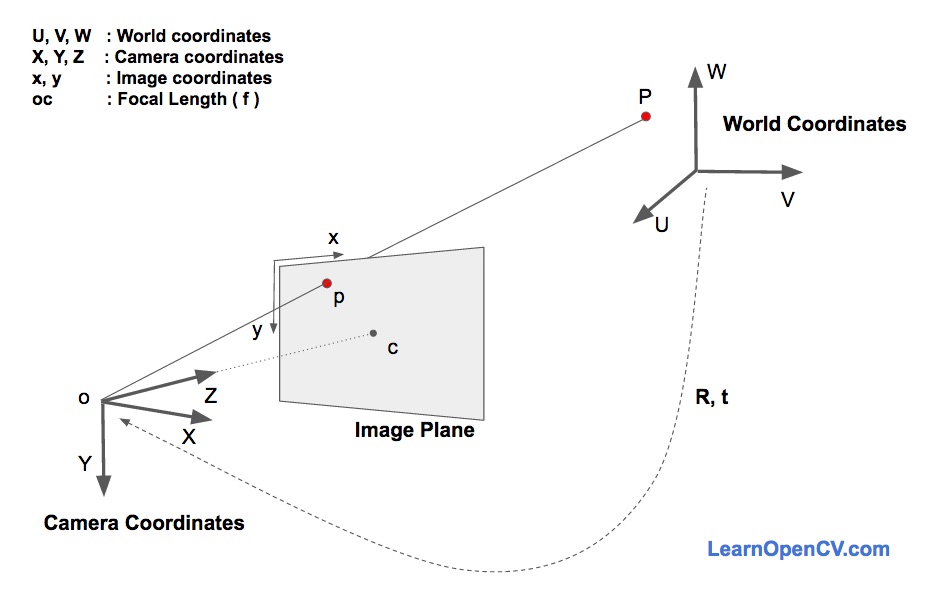
下面,我们来深入研究图像生成方程,以理解上述三个坐标系是如何工作的。
在上述图片中,左下角的O 是相机的中心,中间的平面Image Plane 就是像平面,我们感兴趣的是找出“将3D 点P 投影到像平面中点p 的方程式”。
首先,我们假设已经知道了位于世界坐标系中3D 点P 的位置(U,V,W ),如果我们还知道了世界坐标系相对于相机坐标系之间的旋转矩阵R 和平移向量t, 通过下面方程式,就能计算出点P 在相机坐标系下的位置(X, Y, Z)。
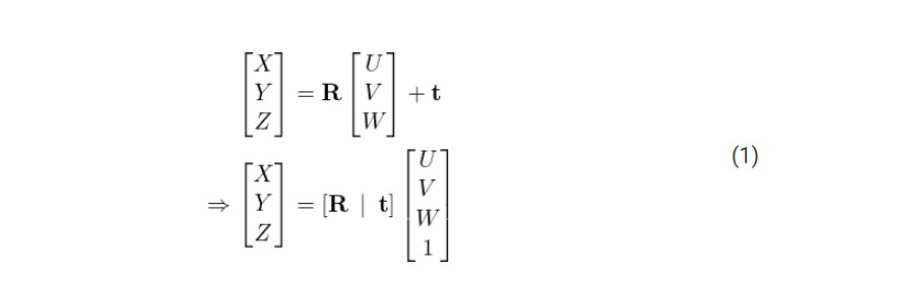
将上面的方程式(1)展开,我们得到下面的形式:
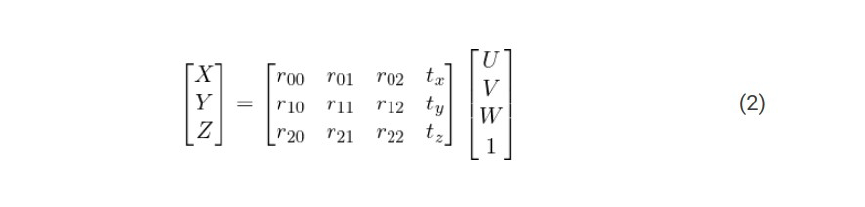
如果学习过线性代数,就应该知道:对于上面方程,如果知道了足够数量的点的对应关系【(X, Y, Z )和(U,V,W )之间的对应关系】,那么上面的方程(2)就算一个线性方程组,其中, rij 和(tx, ty, tz) 就是未知数。运用线性代数的知识,就能解出这些未知数。
正如将在下面章节讲述的,我们知道(X, Y, Z) 只在一个未知的尺度上【或者说(X, Y, Z)仅由一个未知的尺度所决定】,所以我们没有一个简单的线性系统。
5、直接线性变换(Direct Linear Transform)
我们已经知道了3D 模型【世界坐标系】中的很多点【也就是(U,V,W )】,但是,我们不知道(X, Y, Z) 。我们只知道这些3D 点对应的2D 点【在图像平面Image Plane中】的位置【也就是(x, y) 】。在不考虑畸变参数的情况下, 像平面中点p 的坐标(x,y) 由下面的方程式(3)给出。
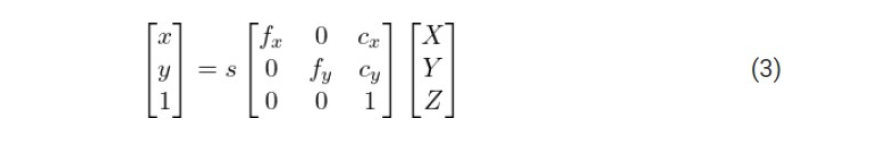
这里, fx 和fy 分别是焦距f 在x 轴和y 轴方向上的长度。(cx, cy) 是相机的光学中心。如果考虑径向畸变参数,那么事情将变得稍微有点复杂了。所以,为了简单起见,我们忽略了径向畸变参赛。
方程式(3)中的s 是什么? 它是一个未知的尺度因子scale factor 。由于在图像中我们没有点的depth 信息, 所以这个s 必须存在于方程中。引入s 是为了表示:图2 中射线O-P 上的任何一点,无论远近,在像平面Image Plane 上都是同一个点p 。
也就是说:如果我们将世界坐标系中的任何一点P 与相机坐标系的中心点O 连接起来,射线O-P 与像平面Image Plane 的交点就是点P 在像平面上的像点p, 该射线上的任何一点P ,都将在像平面上产生同一个像点p 。
现在,上面这些讨论已经将方程式(2)搞复杂了。因为这已经不是我们所熟悉的、能解决的一个“好的线性方程”了。我们方程看起来更像下面的形式。
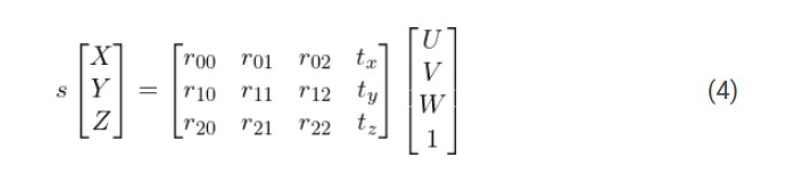
不过,幸运的是,上面形式的方程,可以使用一些“代数魔法”来解决—— 直接线性变换(DLT)。当你发现一个问题的方程式“几乎是线性的,但又由于存在未知的尺度因子,造成该方程不完全线性”, 那么你就可以使用DLT 方法来求解。
6、列文伯格- 马夸尔特优化算法( Levenberg-Marquardt Optimization)
由于下面的一些原因,前面阐述的DLT 解决方案并不能非常精确地求解。第一: 旋转向量R 有3 个自由度,但是DLT 方案中使用的矩阵描述有9 个数,DLT 方案中没有任何措施“强迫估计后得到的3X3 的矩阵变为一个旋转矩阵”。更重要的是:DLT 方案没有“正确的目标函数”。的确,我们希望能最小化“重投影误差reprojection error”,正如下面将要讲的。
对于方程式(2)和方程式(3),如果我们知道正确的位姿(矩阵R 和向量t),通过将3D 点投影到2D 像平面中, 我们能预测到3D 面部点的2D 点在图像中的位置locations 。换而言之,如果我们知道R 和t,对于每一个3D 点P,我们都能在像平面上找到对于的点p。
我们也知道了2D 面部特征点【通过Dlib 或者手工点击给出】。我们可以观察被投影的3D 点和2D 面部特征之间的距离。当位姿估计结果是准确的时候,被投影到像平面Image Plane 中的3D 点将与2D 面部特征点几乎完美地对齐。但是,当位姿估计不准确时,我们可以计算“重投影误差reprojection error” —— 被投影的3D 点和2D 面部特征点之间的距离平方和。
位姿(R 和t)的近似估计可以使用DLT 方案。改进DLT 解决方案的一个简单方法是随机“轻微”改变姿态(R 和t),并检查重投影误差是否减小。如果的确减小了,我们就采用新的估计结果。我们可以不断地扰动R 和t 来找到更好的估计。尽管这种方法可以工作,但是很慢。可以证明,有一些基本性的方法可以通过迭代地改变R 和t 的值,从而降低重投影误差。—— 其中之一就是所谓的“列文伯格-马夸尔特优化算法”。
7、OpenCV 中的位姿估计
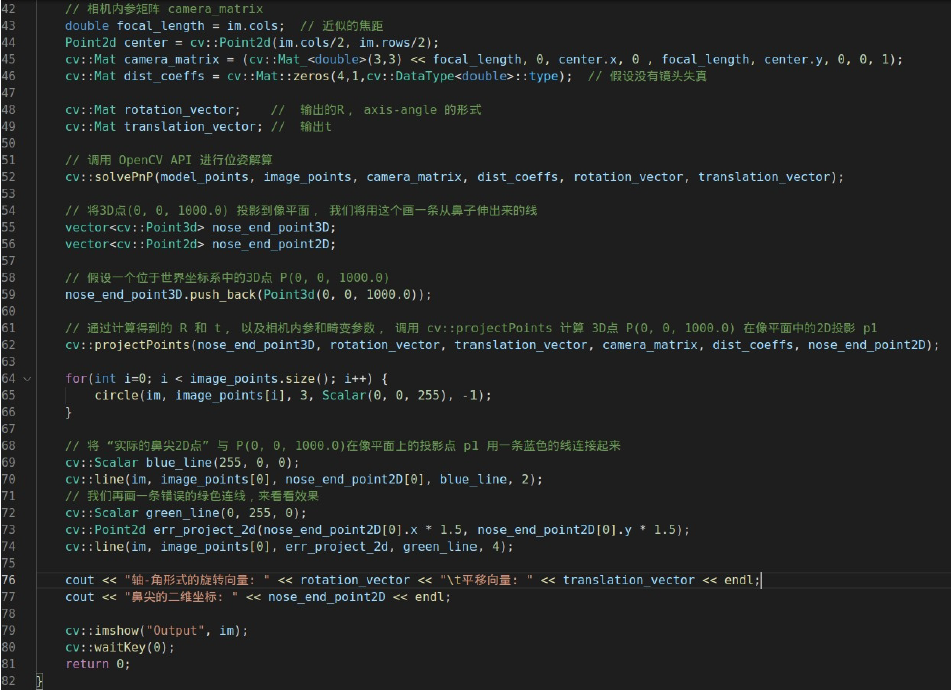
在OpenCV 中,有两种用于位姿估计的API: solvePnP 和solvePnPRansac 。
solvePnP 实现了几种姿态估计算法,可以使用参数进行选择不同的算法。默认情况下,它使用标志SOLVEPNP_ITERATIVE,其本质上是DLT 解决方案,然后是列文伯格-马夸尔特算法进行优化。SOLVEPNP_P3P 只使用3 个点来计算姿势,并且应该只在使用solvePnPRansac 时使用。在OpenCV 3 中, 引入了SOLVEPNP_DLS 和SOLVEPNP_UPNP 两种新方法。关于SOLVEPNP_UPNP 有趣的事情是,它在估计位姿是,也试图估计相机内部参数。
solvePnPRansac 中的“Ransac” 是“随机抽样一致性算法Random Sample Consensus” 的意思。引入Ransac 是为了位姿估计的鲁棒性。当你怀疑一些数据点是噪声数据的时候,使用RANSAC 是很有用的。
8、样例
CMakeLists.txt 文件:
图片文件:

源代码: